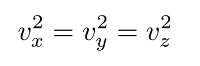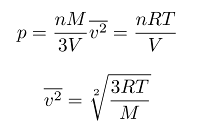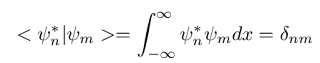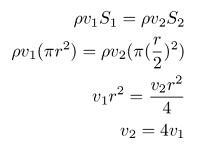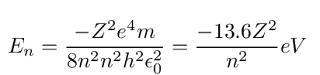Physics GRE Solutions
Here I have written out my solutions to the Physics GRE 0877. For those of you out there studying for the PGRE, I hope this is helpful!
Physics GRE 0877 Solutions
1. (B) Once the ball is thrown out of the car the only force acting on it is the gravitational force. This force pulls the ball vertically downward, toward the earth. However, the ball had an initial velocity in the Southeast direction (vector addition). As no forces are acting on the ball in the horizontal plane this initial velocity is maintained (Newton’s First Law). Therefore, from viewed above, after the ball is released, it travels in the Southeast direction as viewed from above.
2. (D) This is a projectile motion question. Establish the following coordinate system (or another one, just be consistent):
The key to projectile motion questions is establishing a coordinate system and remembering that motion along one axis is independent of motion along another axis. In this problem it does not matter that the object was thrown with an initial horizontal speed of 20m/s - because we are trying to find out the initial vertical height. Vertical and horizontal motions are not related. So, we have:
Therefore, when the voltage across a resistor is doubled, V in the above equation becomes 2V. However, power is proportional to the square of the voltage, so the power is four times as large. Mathematically, you would have...
4. (E) The direction of the magnetic field created by I1 is given by the right hand rule. More concretely, to determine the direction of a magnetic field from a wire with current, place your right thumb along the direction of the current. Then, curl your fingers towards your hand. The direction that your fingers curl is the direction of the magnetic field.
Now, you need to recall that:
In this case, the charges in the circular wire (equivalently the current) and magnetic field are parallel, which means their cross product is zero. Therefore the magnetic field acting on the circular wire is zero.
5. (A) In 1924, French graduate student, Louis de Broglie, defended his thesis concerning the wavelength of massive particles. Enchanted by Relativity and the Photoelectric effect, he developed his own equation for the wavelength of a massive particle.
So, the wavelength of a massive particle is the quotient of Planck's constant and the momentum of the particle.
6. (E) Here you must recall all the Quantum number rules...
Principal Quantum Number (n): describes the shape of the orbital
ranges from 1 to infinity
Angular Quantum Number (l): describes the shape of the orbital
gives total angular momentum (L = (h_bar)^2(l(l+1)))
ranges from 0 to n-1
Magnetic Quantum Number (m_l): specifies specific orbital
gives the projection of L onto a specific axis (L_z = m_l*h_bar)
ranges from -l to l
Spin Projection Quantum Number (m_s): ranges from -S to S (S is the Spin Quantum #, 1/2 for leptons)
So, in this case we are dealing with electrons, so S = 1/2. In the n = 1 shell, there is one s orbital that contains two electrons. In the n = 2 shell, there are an s and p orbital. The p orbital contains six electrons and the s orbital contains 2 electrons. Total the n = 1 and 2 shells store 10 electrons.
6. (C) This question calls for Thermodynamics. Consider a box of dimensions L x L x L filled with n moles of an ideal gas (see figure below). These molecules move in all directions with varying speeds. However, whenever a molecule hits a wall its momentum changes.
Its initial and final momentum before and after the collision are given by:
The time required for a particle to rebound off the right wall, collide with the left wall, and return to the right wall is:
We can now use this time to determine the average force exerted by the wall on the particle during that time period...
For n moles of gas, this force becomes...
And pressure is just the force exerted per unit area....
Now, we recall the definition of the average square velocity...
This means pressure is...
Now, an essential insight is realizing there is no "preferred" direction in this system. Which mathematically means...
And now we can find the RMS speed:
8. (D) Here the Stefan-Boltzmann Law must be recalled. This law states that the total power radiated by a body is proportional to its temperature raised to the fourth power.
In the above equation, A is the surface area of the object, epsilon is the emissivity of the object (which is the ratio of the energy radiated of a given object to that of a black body at a specific temperature), sigma is Stefan's constant (5.67E-8J/sm^2K^4).
In this case, the temperature is increased by two, this means the power radiated is 16 times as large (2^4 = 16). So the mass of ice that can be melted is 16 times as large as well, as power is the amount of energy released per unit time. If the energy released is 16 times as large the mass of ice that can be melted is also 16 times as large.
9. (E) Here Kepler's Laws must be recalled. Kepler's First Law states that the orbit of every planet is an ellipse with the Sun at one focus. His second law states that the line joining the planet and the sun sweeps out equal areas in equal time periods. His third law states that the square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit.
10. (B)This is all about energy. We know the potential energy stored in a spring is given by PE = (1/2)kx^2, where x is the compression of the spring. And as usual, the kinetic energy is KE = (1/2)mv^2. If you would like the ball to reach a velocity of v, this amount to saying the all of the potential energy of the spring becomes the kinetic energy of the ball.
11. (C) This is not one you would want to derive by hand. You just want to remember that:
12.(C) In the late 19th century, scientists discovered that the radiation emitted by Hydrogen atoms (as well as others) was only emitted at specific quantized frequencies. In 1913, Bohr tried to explain this with his theory of the Hydrogen atoms. His theory was founded upon the following four postuates:
1) Electrons move in circular orbits subject to the electromagnetic forces (for the attraction of the electron to the nucleus) and classical mechanics.
2) There are not an infinite number of orbits that an electron may occupy. Electrons can only be in orbits were its angular momentum is an integer multiple of h (L = nh).
3) The energy of an electron in an orbit is constant, despite the fact that it is accelerating.
4) An electron only radiates electromagnetic energy of f = (E2-E1)/h. Emitting this specific energy allows the electron to jump down to a lower energy orbit.
Mathematically, this becomes:
An electron moving in a stable circular orbit around the nucleus (Newton's Second Law).
Additionally, the only force acting, the Coulomb force, is central so angular momentum is conserved.
Now, linear momentum is just:
And, you can also check units and use your common sense. We expect the linear momentum of the electron to decrease at larger n.
13.(A) So the difference between a normal plot and a log-log plot is that .... a log-log plot takes the log of x and the log of y and plots those against each other instead of just x and y. This means that an equation like y = ax^m, where a is the y-vale at x = 1 (you can double check that), will be a line on a log-log plot. Since, we have a case like that here, that is the general form of the equation. Now, to dig into the math....
We know a = 6 since the y-value at x = 1 is 6. Now, we have to find the slope.
Just as the slope of a line on y vs. x is the change in y over the change in x. The slope, m, on a log-log plot is:
Using the points, (3, 10) and (300, 100), m is found to be 0.5. So, y = 6x^(1/2).
14. (B) This requires some experimental technique, that I did not remember. So, here we go...Say I take N separate measurements of a quantity:
Then, the best estimate of the value of x is the weighted average, defined below.
The uncertainty of the weighted average is:
15. Here you want to recall the equation:
R1 is the radius of the lens closest to the light source. R is positive if the center of curvature lies on to the left of the light source. So, for (A) R1 = -R, R2 = R, so F~-R/2, (B) F~ -R, (C) F~R, and for (D) and (E) F~R/2, but R is smaller for (E). Therefore, (E) is the has the shortest focal length.
16. (D) This is an application of Malus' Law:
Here I_0 is the initial intensity of light passing through a polarizer, and theta is the angle between the initial polarization (plane of the electric field) and the axis of the polarizer (the plane containing the slit of the polarizer).
In this case, after the light passes through the first polarizer it's intensity, I1, is:
After passing through the second polarizer, I1 is halved. So, the final intensity is 25% of the initial intensity.
17. (A) Well, here you can rule out (B) - the electric field will decrease as r increases. From, there it is difficult to guess. So, its time for physics : ) Recall, Gauss' Law?
Here if we take a Gaussian cylinder, of length l, around the line of charge we have a surface of constant electric field strength.
18. (E) This is Lenz's Law...as the magnet enters the loop it increases the flux going through the loop towards the circuit. So, nature does not like change - it fights to maintain the past. This translates to a counter current in the direction of b to a to balance this increase in flux. When the magnet moves back away from the loop the direction of the current in the circuit is reversed in order to counteract the reduction of magnetic flux, due to the retreating motion of the magnet.
19. (A) Wien's Law!
20. The temperature of the universe depends on the cosmic scale factor as follows:
So, taking a ratio of the temperature at 12K and 3K, you find...
Here the two subscripts refer to the circumstances now and the one subscripts refer to the past.
21. (C) Here you must recall for adiabatic processes (quick - no heat transfer):
Also, using the ideal gas law to substitute P = nRT/V gives answer (C).
As a side note for the curious, the adiabatic relation can be derived as follows:
Take the derivative of the ideal gas law:
Apply the first law of Thermodynamics:
Use the definition of the Specific Heat at constant volume:
But, what we want is ndT....
And we need one more relation...
Substituting the last two relations into the first equation...
22. Relativity! This problem requires three equations....
Then, using the conditions provided....
23. (B) Relativity, again! So, we know the meterstick is contracted to a length 0.6m as seen by one of the spaceships. From this information we can find gamma using the length contraction formula:
Here L0 is the length of an object in its rest frame and gamma is defined in (22).
Using this equation we find gamma to be 5/3. Now we need to find v, in this case the relative velocity of one spaceship to the other as measured in their own reference frames. This requires the velocity addition formula:
First we must arrange our reference frames in order to use this equation. Let S' be the reference frame of the ship to the left of earth and S be the Earth's reference frame. Their x-axes are aligned and point in the positive direction to the right of the Earth. Then, let u' be the velocity of the spaceship on the right in the S' reference frame, u is the velocity of the spaceship on the right in the Earth's reference frame, and v is the velocity S' relative to the Earth's reference frame. Mathematically, this means u = -v. So, the above equation becomes:
In units, where c = 1 this simplifies to:
This is the velocity that the spaceship on the right approaches the one on the left in S', meaning it is the "v" in the gamma formula. Combining these two formulas:
(Once again, these are units where c = 1.) In the above formula "v" is really u', the relative velocity of the two spaceships...
Solving this, you should get v = 0.5, which is really 0.5c.
24. (B) Well, the PGRE was not one for variation on this page. Yet another problem about mechanics at the speed of light. So, this meterstick is flying by at 0.8c (How? Who knows.) This means its length is contracted...
Now, it is back to simple mechanics to determine the time required for the meterstick to pass the observer:
BOOM. We are done! Take that relativity!
25. (E) Well, this comes down to Quantum Mechanics and if you zoned out for that (like me) here is a refresher! For two states to be orthogonal you want their dot product to be 0. Back in the day, that is Calculus class, dot products were simple things.
However, the dot product is just a special case of the inner product of two vectors. So, representing two wave functions in bra-ket notation the inner product is:
The last equality only holds if the two wavefunctions are orthogonal.
26. (D) Ok, so you could use common sense, the Bohr radius is defined as the most probable distance between the electron (in the ground state) and proton in Hydrogen. But, if that does not come to mind - it's time for math! Let the probability that the electron is found between r and r + dr = P.
We know from Calculus the maxs and mins occur when the first derivative is zero. So, let's set it to zero and solve.
Solving this, you should find r = a0 is where the maximum occurs. You could go ahead and check the second derivative to insure that a0 is a maximum not a minimum, but most people do not have time to do this.
27. (C) This is an application of the Energy-Time Uncertainty Principle.
Solving the last equation, you should get the variation in frequency to be approximately 500MHz which is closest to (C).
28. (D) The work done by a spring is:
So, the work done, W1, to stretch the first spring a distance x is:
The work done to stretch the second spring, half the distance of x is 2W1:
Solving this last equation, (D) is obtained.
29. (C) Well, in elastic collisions kinetic energy is conserved so.....
Where b is the speed of the second block. Solving this equation for b, one obtains (C).
30. (D) This is one you want to have committed to memory. You can also simplify this to the one dimensional case, where:
Then, the first equation states that the derivative of the Hamiltonian w.r.t. momentum, which is p/m, is the velocity - and that is true. The second equation states that the negative derivative of the Hamiltonian w.r.t. position, -dV/dr, is the derivative of momentum, or the force - and that is true.
31. (C) This is an application of Archimedes principle, which states that the buoyant force acting upon an object is equal the the weight of fluid it displaces. The diagram below illustrates how the buoyant force is defined.
In this problem, from Newtonian Laws we know the Buoyant force must be equal in magnitude to the Force of Gravity (weight) of the block. Then, from Archimedes principle we know the buoyant force is equal to the weight of fluid displaced:
32. (A) Bernoulli's principle! So, let's derive it like real physicists : )
Imagine the following setup. At position #1 you have a volume element with area A1. At position #2 you have the same volume element but with a different area, A2.
At position #1 the total mechanical energy is:
At position #2 the total mechanical energy is:
But, wait a second. What if ME2 is not equal to ME1. What does that mean?!?!?!?
It means work was done on the system. The initial work done on the system might have been done by a pump, dwarf, or god knows what. So let's call that W_on:
Similarly, the work the system is doing is given by W_out:
You can imagine W_on is the initial work done on the system (by a pump or some other device) and W_out is the work the system can do after passing position #2. The difference between W_out and W_on is the change in mechanical energy of the system.
And that last equation is Bernoulli's equation. BOOM!
So, in this question we also need to remember that mass is conserved. This is exemplified by the following equations, which states the the flow rate is constant. This means there is no buildup of fluid. :
Now, substitute this into Bernoulli's equation. We can eliminate the gravitational terms as y1 is the same as y2.
33. (E) Thermodynamics time! You thought you would escape, but little did you know.
So, we need to recall the fundamental Thermodynamics relationship, which we will derive!
First Law of Thermodynamics: The change in the internal energy of a system is equal to the heat added to the system and the work done on the system.
We also know that in a reversible process the change in entropy is the quotient of the heat exchanged and the temperature.
Now, using this equation to substitute dq = TdS in the previous equation we find the thermodynamic identity:
Solving for the entropy change:
Assuming that water is an incompressible fluid (i.e. its volume does not change) dV = 0. Also, we know that no work is done on the system, only heat is added. This means dU = dq = mc*delta(T)...
Integrating both sides, (E) is obtained.
34. (C) For the first case, we can use the First Law of Thermodynamics to determine the change in internal energy:
The change in internal energy simplifies to just Q as the volume is constant which means that there is no pressure-volume work done (PdV = 0 as dV = 0). Now, we want to relate this change in internal energy to a change in temperature. We can do this with the equipartition theorem:
Also, it is useful to recall the relationship of Nk and nR...
Now using these two relationships, let's take the differential of the equipartition theorem for a monoatomic ideal gas (three degrees of freedom):
Using this information we can tackle the constant pressure case. For constant pressure, the change in internal energy is given by:
But, we also know that the change in internal energy must be the same in the constant volume case as the change in temperature is the same - and internal energy and temperature are directly related through the equipartition theorem.
So, the last thing left is solving for PdV in terms of nRdT. Well, that is just the ideal gas law:
So, that takes quite awhile. Thankfully, you can always do a sanity check. We expect the amount of heat required to heat a constant pressure system to be greater than one of constant volume, as some of the energy will be used to expand the volume of the gas.
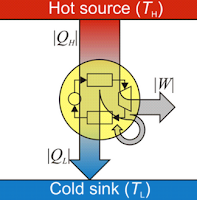
35. (B) Time to talk about heat pumps! A heat pump is a device applies work to extract heat from a cold resevoir, Q_c, and delivers heat, Q_h to a hot reservoir.
 Heat pumps are characterized by the coefficient of performance (COP), which is just the ratio of the heat given to the hot reservoir and the work required to provide that heat.
The most efficient and unattainable heat pump is a Carnot Engine (2 Isothermal steps and 2 Adiabatic steps). For a Carnot Engine, each step is reversible - no entropy is produced. This simplifies the COP as follows:
The last line comes from the fact that since no entropy is produced, |S_H| = |S_C|.
Now, equating these two equations and putting the temperatures in Kelvin - this is very important - (B) is obtained.
As a side note, efficiency, e, often comes up when engines are discussed.
For heat engines the efficiency is:
Heat engines look in general like this:
This efficiency of a heat engine is always less than the Carnot efficiency which is:
36. (A) Time to switch our focus from heat to charge! So, first let's figure out what the current looks like through the circuit using Kirchhoff's Voltage Law (KVL). You might first want to recall the how the voltage across a capacitor and inductor vary with charge and current:
Now applying KVL to this circuit:
The next step, which will not seem terribly intuitive - because it is not - it is just born out of the fact that solving this differential equation any other way would be very ugly - we are going to take the time derivative of the last equation to solve for i. You could also think of it as - we need have all i's or q's - this is easily accomplished by taking the time derivative and solving the resulting ODE.
Lastly, we must figure out the energy stored in the inductor. Recall that the energy stored in an inductor is proportional to the current squared. For a capacitor the energy stored in it is proportional to the voltage squared (Fyi).
Omega is the square root of L*C.
37. (E) Time for vectors! Just when you thought you had escaped : D So, let's start with some labels...
Now, from here just be careful with the vectors. We know the y-components of the electric field of the positive and negative charges will cancel each other. The x-components add though...
38. (E) Ok, no need for numbers here, just sanity. Using the RH rule we know the magnetic field of the vertical wire will be into the page and the field from the horizontal wire will be out of the page. Moreover, we know the magnitude of the magnetic field of a wire is given by Ampere's Law:
And this is all to say that the magnetic field of a wire only varies with the current it carries and the distance from the wire. So - the magnitude of the magnetic field from each wire is the same - they are just pointing in opposite directions - therefore the total magnetic field is zero.
39. (C) So - not everything is relative, but a hell of a lot is. Einstein started all this relativity business. In fact, he basically declared everything to be relative - EXCEPT - the speed of light. That is a constant. It does not matter if you are standing still or driving down the highway at 0.8c - the speed of light will always be c.
I feel it is vital to explain what it means for something to be "relative" in physics - because it definitely took me awhile to figure out. So, let's take the example of looking at your best friend for 10 feet away. They may seem very sad from 10 feet away. However, looking at them from 100 feet away these details - facial expressions are blurred. They may seem estatic at that distance. Then start moving while you are looking at them - and everything is shot to heck.
To say that something is relative is to say that the measurement or observation varies between reference frames.
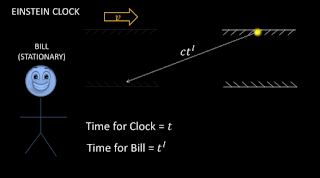
Back to the speed of light being constant. This seems like a simple axiom - right? I mean it is - but its consequences are far from anticipated. Let's take a look at an Einstein clock, which is composed of two mirrors facing each other with light bouncing between them. Like this:
So, we've got Bill standing still and measuring time as t_l while the time of the clock is measured as t. Now, let's imagine that the clock moves to the right with a velocity v.
So, in the clock's reference frame it moves a distance ct, but in Bill's reference frame he sees the light move not only vertically but also horizontally - so it moves a total distance ct_l. Now, using pythagorem Theorem we can resolve t_l and t.
Now, gamma is always equal to or greater than one, which means that Bob always measures the time it takes the light to move from one mirror to the other to be longer that someone moving with the clock would.
So this same phenomenon of time dilation of events occuring in a moving frame w.r.t. a stationary frame apply to muon decay. In this case, the decaying muon is the moving particle so it measures time as t. The lab frame - is Bill's frame. Gamma is 5/3 for this problem, which makes the lifetime of the muon in the labframe = gamma*t = 3.7*10^-6. The distance an object travels is just d = vt. Multiplying that out you should get ~880m (C).
40. (B) So, what is vital to solving this problem is recalling a less well-known equation from Relativity:
From here, you first should apply the conservation of momentum - as the initial momentum is zero the momentum of the massless particle and the massive particle have to be equal in magnitude, but opposite in direction. And let's solve this in units, where c = 1 and recalling that the energy of a massless particle is pc - or just p in units were c is 1. Substituting this knowledge into the above equation, you should find:
Solving this equation for p, you should obtain (B).
41. (B) One equation you want to have committed to memory is:
The equation relates to the Photoelectric Effect, brought about by Einstein and others in 1905. hv is the energy of the incident light and W is the work function of the material (the amount of energy required to remove one electron from a given material. So, Einstein thought "hey maybe light is also particle-like, not just wave-like" after seeing the results of the Photoelectric experiment. In this experiment a metal is illuminated with light (photons) and electrons are consequently ejected from the metal because of this. These "photoelectrons" are gathered on a plate. The metal and the plate are joined electrically to form a circuit. So, the gist is that the strength of this photocurrent can be measured through the wire connecting the plates. A potential can be applied between the plates to stop this current as well. To stop the current entirely requires the potential to be equal to the stopping potential in the above equation, V_0.
So, some scientists thought if you increased the intensity of the light (or the number of photons hitting the metal per second) that current would increase, but this was not found. In fact, the intensity of the light had no effect. Also, there would be no current below a certain "cutoff frequency."
These misunderstandings lead to a new theory. Light is composed of particles with discrete amounts of energy. Thereby, the photoelectric current depended upon the energy of the light (which is directly related to the frequency of the light).
Rearranging the first equation by solving for V_0 - the slope of the graph is h/e.
42. (E) The horizontal distance between to points with on the graphs corresponding to the same point in the wave is about 2cm, but a complete cycle of the wave spans about 6cm. From here, you can just set-up an equality to determine the phase difference. We know the period of a sin wave is 360 degrees...
Solving this you should find the phase difference to be approximately 60 degrees.
43. (D) This is something you should have learned in an elementary solid state physics course, but if you did not - here it is now. So remember it : )
In the diamond structure of elemental carbon the nearest neighbors of each C atom lie at corners of a tetrahedron.
44. (D) BCS Theory explains superconductivity. It was developed by John Bardeen, Leon Cooper, and John Schrieffer in 1957, hence the name. Superconductivity is a property some materials exhibit once they are cooled to their critical temperature. At this temperature and below it, the material exhibits no electrical resistance. BCS theory explains this phenomenon as the production of Cooper pairs. Below T_C lattice vibrations are minimal, so the lattice of the material looks something like this:
As one electron moves through the material it attracts the two positive charges above and below it towards itself. However, this motion of positive charges is delayed so that the electron moves past the positive charges before they move together. Once the charges do move towards each other they are repelled by each other but leave behind a positive charge region which attracts the next electron behind it. These two electrons moving through the lattice are called a Cooper Pair - and they do not interact directly with the lattice and therefore do not experience any electrical resistance to their flow. And this is what explains superconductivity in metals (but not Cuprates, which have a higher T_C. Their superconductivity is still an active area of research and might be explained by anti-ferro magnetism).
45. (C) Doppler effect! This should have been a problem you anticipated. Here is the formula:
v is the velocity of the waves relative to the medium, f is the emitted frequency, v_receiver is positive if the receiver is approaching, v_source is positive if the source is receding. In this case, the source and the receiver are not moving - so there is no Doppler Effect - f_obs = f.
46. (D) Here you just want to recall the conditions for a minimum for single-slit interference:
**Note: These are the maxima for double-slit interference. And for a circular aperture, the first minimum is given by:
Anyway, back to this problem. We know we are looking for the first minimum produced by single-slit interference of sound waves which obey the normal velocity, frequency, wavelength relation:
So, solving this equation for wavelength:
Now, substituting this into the first equation:
47. (D) Here you need to recall the harmonics of a tube open at only one end. (Here is a video about harmonics for a tube with two closed ends.)
Keep in mind there are only odd harmonics (odd n values) for a one-end tube. So, the next harmonic for a one-end tube will be the third harmonic which will have a frequency three times as great as the fundamental harmonic.
48. (C) Here are the basic components of logical circuits that you need to know!
An AND gate adds the inputs, an OR gate multiplies the inputs, and a NOT gate flips the input from 1 to 0 or 0 to 1.
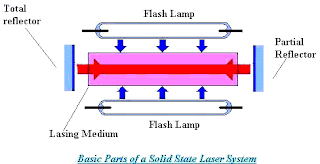
49. (D) Time to review types of lasers....
So a diode laser has a laser diode in it, which is composed of two semiconductors. One is a p-type semiconductor (which wants electrons - it has a "hole") and the other is a n-type (it has extra electrons). When a current passes through this pn junction it excites one of the electrons for the n-side to go to the p-side. However, the hole on the p-side is at a lower energy, so the electron must lose some of its energy by emitting a photon to stay in the hole. This photon is trapped in the pn junction as there are mirrors on both sides of the gap. This trapped electron than excites other electrons to move to the p-side and produce more photons. All of the released photons have the same phase, polarization and travel in the same direction producing laser light. This light is than collimated. This video also explains diode lasers. So - no free atoms involved here.
Dye lasers use an organic dye as the medium. They are highly tunable.
In a free electron laser a beam of free electrons are excited by a magnetic field.
A gas layer is comprised of a gas that has current flowing through it. This current excites molecules to higher energy levels. When the molecules decay back to the lower energy level - light is given off...
And a solid state laser has a lasing medium that is solid:
So, it is obvious that the only laser with free Atoms (not just electrons) is the gas laser - as atoms in a gas can be pretty accurately modeled as ideal gases.
50. (C) You could use dimensional analysis here, but just knowing it by heart is probably best. To derive it use:
First, eliminate v and solve for r in terms of n [r_n = (n^2 h^2)/(kmZe^2)]. Then solve for the kinetic energy by using the first equation and eliminating v. The potential energy is just kZe^2/r, adding this the the kinetic energy and removing r's with the equation found earlier one should find the energy levels to be:
51. (D) Atoms only emit and absorb specific frequencies - meaning II is false, but I is true. At low temperatures, the atom is in the ground state. Any light the atom could absorb from this state would boost its energy to an excited state. It would emit the same frequency of light if it decayed back to the ground state - III is true.
52. (C) Bragg diffraction! So crystals have a very regular structure. Something like this:
Guess what happens when light hits it like this:
Yep, you guessed it diffraction! Since crystal atoms are generally an angstrom apart - X-ray light will diffract off crystals. So let's get into the math. Let's determine the condition for constructive interference. Well we know the path length difference will have to be an integer multiple of the wavelength. And the path difference here is given by:
And, there you go the condition for constructive interference from a crystal through Bragg Diffraction. Substituting the numbers in you should get (C).
53. (D) Here is the theme of the PGRE in case you have not noticed: ask questions that seem much more difficult than they are. Here you don't need to remember Kepler's Laws or too much of anything other than the definition of angular momentum and the velocity of an object in circular/elliptical motion.
Now, we know the angular momentum of both planets are the same and the magnitude of the angular momentum is mvr as the velocity and radius are perpendicular.
54. (E) A solar mass black hole would attract the planets no more than the sun, so there orbits would be unaffected.
55. (A) Time for the Doppler Effect gone Relativistic! Ok, so if you want to derive it on the exam that is probably not wise. But for your reference, here is the derivation. We are just going to use the result for now:
Beta is positive if the source and observer are approaching one another, f_0 is the observed frequency and f_s is the emitted frequency. So, using this and the fact that c = wavelength * f, you should get (A).
56. (D) Tricky kinematics! So, it is best to start with a picture...
There are two parts of this question which are not immediately obvious: (1) in order for the plane to head North the pilot must aim the plan in the NW direction (2) the pilot is flying at 200km/hr in the NW direction, not the North direction - that is impossible.
Now, using the Pythagorean equation you should find the velocity in the N direction to be 10sqrt(391). Then, just use t = d/v to find the time required to fly 500km in the north direction.
57. (B) Ok, so guess what another tricky kinematics equation! First, let's figure out the acceleration of the system:
So, in the first figure, for the mass m block to accelerate at F/3m the force acting on it (F_12) has to be F/3:
In the second figure, for the mass 2m block to accelerate at F/3m the force acting on it (F_12) has to be 2F/3:
58. (A) The only force providing acceleration for block B is the static frictional force. Therefore, F=ma = 10*2 = 20N.
59. (C) Well we know the period, and yes you should know this, of a pendulum is:
However, this pendulum is accelerating upward at a. So, in the above equation g represented the net acceleration of the pendulum, which is now -g+a. This site explains a bit of how the period changes. Basically, the effective acceleration, which replaces g in the above equation, when the pendulum is accelerating is given by g' = g-a, where the downward direction is positive. In our case that leads to g+a = g'. Substituting that into the above equation gives (C). You can also see that all the other answers are not physically realizable. (A) a will effect the period, (B) the period will blow up at a = g - that is not right (C) is right, (D) a = 0, T = 0, wrong, (E) blows up at a = 0 - wrong.
60. (C) Ok, so this one is slightly tricky, but just take a breath and your time and you should get through it just fine. We know the field due to the middle wire (lying along the x-axis) is just:
Now, the other two wires are the same radial distance from the y-axis at a given y-value. And they also both add constructively - remember the RH Rule? I sure hope so! So the radial distance of the the wire pointing in the NE direction to the y-axis is:
Turns out the radial distance of the wire pointing in the SE direction is the same. Now, we just need to add up all the fields:
61. (E) Ok so you could know all about mass spectrometers or just derive the relationship between r and q/m...
A moving charge entering the magnetic field region will experience a force:
In this case v and B are orthogonal, so this simplifies greatly. Also, the particle will undergo circular motion as the force is orthogonal to the velocity (a condition for circular motion).
So, from here it should be clear that when the q/m ration is doubled R is halved.
It is also worthwhile to mention here how velocity selectors work.
 |
| http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/maspec.html#c2 |
62. (E) Gauss's Law! You better remember it or .... you might want to toast your PGRE instead of take it. I mean who knows, maybe it will be tasty. See food printers :D
63. (D) This is an example of beta plus decay (a.k.a. positron decay). Positron decay happens in nuclei with too few protons. In this reaction p -> n + e+ + antineutrino. This decay is mediated by the weak force.
64. (D) Quantum again! You better know these equation as well. The eigenvalues of L^2 and L_z are:
Using the given L^2 value you should find l = 1. This means m = -1, 0, 1 - therefore the possible L_z values are -hbar, 0, and hbar.
65. (C) Well we know the energy levels of the quantum harmonic oscillator are given by:
So, yeah they are evenly spaced energy levels - (I) is true. The potential energy is not linear it is quadratic E = 1/2 kx^2; (II) is false. The ground state has an energy 1/2 hbar*omega - not zero - (III) is false. But there is a nonzero probability for the particle to exist outside the classical turning point because it is quantum mechanics - you should be able to prove this - but don't do it on the exam. You do not have time. (IV is true.)
66. (D) The energy levels in the Bohr atom are proportional to the reduced mass of the system. And reduced mass is:
So we need to multiply by mu _ muon sys/ mu _ hydrogen atom to have the energy for the muon system.
So this is multiplied by the energy levels which gives (D).
67. (D) Wow, two D's in a row.... so the electric field inside a capacitor is
And sigma is just q/A, so...
Now, just substitute in the given quantities, A = (0.5m)^2 = 0.25m^2, i = 9A.
68. (D) Wheatstone bridge - or at least nearly one! No current will flow through the two horizontal resistances because the current split will be exactly the same as it was for the three resistors the current just went through.
69. (D) Here you want to use impedance to solve. We know the total impedance of the circuit is:
We also can determine V_0 and then solve for the ratio of V_0/V_i:
So as omega -> infinity the ratio approaches zero. At omega = 0 the ratio is 1. This matches (D).
And sticking our head up above the math this makes sense. The voltage across a capacitor decreases monotonically as frequency increases. Only (D) matches this observation.
70. (A) This is just Faraday's Law.
We know the induced EMF is flowing through the wire due to the change in magnetic flux. We also know that any EMF induced in the wire is subject to V = IR. So....
Now, you can just solve the above equation for q. Be careful to convert 10cm^2 correctly to m^2.
71. (B) This is just an application of uniform circular motion and magnetic forces. So, we know the only force acting on the object is the magnetic force and that is creating circular motion. Therefore, we have:
The last equation is applicable in this case as the magnetic field acting on both particles is the same and they also both have the same charge. So, since R is proportional to v R1/R2 = 1/3 means V1/V2 = 1/3.
72. (D) Fermions have antisymmetric wavefunctions and obey the Pauli Exclusion principle. Bosons have symmetric wavefunctions and do not obey the Pauli Exclusion Principle.
73. (D) Read the first two chapters of Griffiths' Introduction to Elementary Particles.
74. (E) You can use the lensmaker equation or ray trace. I think the latter is faster - but it's up to you.
Here o is the object distance, i is the image distance, and f is the focal length. The focal length is positive for converging lens and mirrors and negative for diverging lens and mirrors. The object distance is positive it the surface that the light first hits has its radius of curvature on the same side as the object. The image distance is positive if it is on the opposite side of where the image distance is positive. Also, note that the image distance is positive for real images and negative for virtual images. In this case, o = -R, f = 2R (always true). Then solving the lens equation, you should find i - -R/3, which means it is virtual and on the right.
The ray diagram looks like this:
 |
| http://hyperphysics.phy-astr.gsu.edu/hbase/geoopt/mirray.html |
As this is a thin film, we approximate that the distance travelled by a light wave that goes through the film and reflects off the bottom and travels back into the air is 2t, where t is the thickness of the film.
The light wave that just reflects off the top of the film undergoes a pi phase change. Therefore, for constructive interference we want the path difference to be an odd multiple of the wavelength/2...
For the shortest wavelength n = 0. This lets you solve for t, 135nm. Then, to find the next wavelength of positive interference set n = 1 and solve the above equation for lambda.
76. (B) This takes a bit of math or just knowing. Either way, it is not terrible. You just need to pay attention to details.
First, apply Snell's Law to the light wave refracting from air into the cable:
Here theta_C is the critical angle for total internal reflection (where the reflected angle is 90 degrees). You can then derive what the critical angle must be using Snell's Law:
Just remember that sin(90-theta) = cos(theta) and solve for cos(theta) using a right triangle based on the above equation. Solving all that you should find that the sin^-1 = sqrt(n^2 -1). Now, the angle must be the critical angle or less as when theta decreases, the critical angle increases, which would still mean that the light ray would reflect internally. Big incident angles are good for total internal reflection : )
77. (C) Here you want to know two equations:
So, the first one is hopefully clear. The second equation states describes the mean free path distance for gas particles. From here we know that t = d/v = l/v_rms. From there you should find v_rms to be proportional to the square root of m.
78. (B) This comes from the Boltzmann (and Gibbs) Distribution.
79. (D) This is really just algebra. First, solve for P:
Then, we know that work is just the integral of negative PdV. Integrating you should get (D).
80. (C) Ok, so we know that for a spring and a mass the frequency of oscillations is:
Using the information for the first case, you should find k = 4pi^2. Then, in the second situtation k = 8pi^2. Using this information you should find f = 1/2.
81. (B) So this is just energy conservation.
And remember that v = omega*r and the moment of inertia for a disc is 1/2mr^2. Putting all that in the last equation above you should get (B).
82. (D) So you have to remember two important things - the Lagrangian and the definition of velocity in polar coordinates:
There is a great derivation of the second equation here. We also know that the potential energy of a spring is 1/2 kx^2. Using that information you should get (D). It is important also, to remember that x in that equation represents the amount that the spring is stretched from its relaxed position.
83. (E) Oh, Hamiltonian Mechanics!!! Here are the relevant equations:
So basically, if the Hamiltonian of a system is independent of a given q_i, then that q_i's conjugate momentum is constant. And vice versa! If the Hamiltonian is independent of a given p_i it's conjugate q_i is constant. So in this case, the Hamiltonian does not depend on phi, so p_phi is constant.
84. (E) So, we just need to turn the algebraic equation for the center of mass into a calculus equation....
Don't forget that lambda = m/L.
85. (B) First, normalize the wavefunction. Doing this you should find A = sqrt(2/L). Then just integrate the wavefunction squared over the interval L/3 to 2L/3. Doing this you should get (B).
86. (B) Eigenvalues will just make the determinant of A-lambda*I = 0. Applying that here you should get (B).
87. (D) Matrix multiplication.
88. (D) First you need to determine the normalization constant. Then, use that to find the coefficients of the up and down spin states.
The probability of being in the down (0, 1) spin state is just the magnitude of the coefficient squared. Giving (D).
89. (D) Time to NOT freak out. This is a rude question, but it is not as bad as it looks. We know that the reflection coefficient is just:
Here, B is the coefficient of the reflected wave, and A is the coefficient of the incident wave. (Technically it is the squared magnitude of the probability current, but here it simplifies to this.) Now, we just have to remember that the wavefunction is always continuous and the derivative of it is continuous whereever the potential is finite. That gives the following relations:
Simplifying those, and solving for the fraction, you should get (D).
90. (D) Here you just need to apply the longer formula for V....
In region I, you just need to integrate from a to r. For region to you need to integrate from a to b. (Outside b, the electric field is zero, so you do not need to integrate there.)
91. (C) Stoke's Theorem. When the curl of a vector field is zero, the line integral around any closed loop is zero. This allow you to describe an unambigious function psi that defines the vector field as the divergence of it.
92. (E) The magnetic field is given by Ampere's Law, stating that the magnetic field is proportional to the enclosed current divided by r. From 0 to R there is no enclosed current, so B is zero. From R to 2R the enclosed current increases. Outside 2R the enclosed current is constant so the B field decays as 1/R. Only (E) matches this.
93.